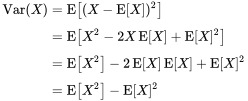백준 17978번 Washer 문제 해설

문제

You have n clothes and a washer. The washer is large enough to wash all clothes at once. However, we should worry about the color transfer: if we put clothes of different colors in the washer, the dye from one may stain another. Precisely, let ri, gi, bi denote the amount of red, green, blue color of the ith clothes. When n clothes are washed together, the color transfer c is defined by

\[c=\Sigma_{i=3}^n{(r_i-r)^2 + (g_i-g)^2 + (b_i-b)^2 }\]

where r, g, and b are the averages of ri, gi, bi, respectively. The i-th clothes with ri, gi, and bi is defined as a point (ri, gi, bi) in 3-dimensional RGB space. You can assume that no three points (clothes) are on a same line and no four points (clothes) are on a same plane in RGB space.

The washer consumes a lot of electricity, and you have to partition n clothes into at most k groups, and run the washer for each group. The total color transfer is the sum of color transfers from each run. Given the color information of n clothes and k, write a program to calculate the minimum total color transfer.

입력

Your program is to read from standard input. The first line contains two integers n (1 ≤ n ≤ 100) and k (1 ≤ k ≤ 2). In the following n lines, the ith line contains three integers ri, gi, bi (0 ≤ ri, gi, bi ≤ 1,000).

출력

Your program is to write to standard output. Print exactly one line containing the minimum total color transfer, rounded to the sixth decimal point.

---

풀이 과정

RGB 3차원 공간 내에 있는 점들을 1개 또는 2개의 그룹으로 묶어서 분산의 최소를 구하는 문제이다.

You can assume that no three points (clothes) are on a same line and no four points (clothes) are on a same plane in RGB space.

우선 이 부분이 왜 있는지 초반에는 이해하지 못했다.

그런데 분산을 구하는 문제이다 보니 같은 그룹 내에 있는 점들이 가까울 수록 정답에 근접하겠다고 생각하는 순간, 왜 저런 내용을 지문에 넣어뒀는지 이해했다.

3차원 공간에서 평면을 생성하여 그 평면을 기준으로 두 그룹을 나누어서 계산하라는 뜻이다.

그리고 해당 평면을 생성하는데에 있어서 예외처리를 안해도 되게끔 적어준 것이였다.

기준이 될만한 공간내의 평면은 3개의 점을 잡아 생성할 것이었다.

N개의 점에서 3개의 점을 정한 후 (${n}C_{3}$) 해당 점을 이용해 평면을 제작해보자

세 점을 고르면 평면이 생긴다.

문제의 지문에 따라 세 점을 고르면 하나의 평면이 생성된다는 것을 알 수 있다.

세 점을 골라 평면을 만들었다면, 어떻게 특정한 점 X가 평면을 기준으로 위쪽 방향에 있는지, 아래쪽 방향에 있는 지 알 수 있을까?

그 해답은 법선벡터에 있다. 우선 세개의 점 ($P, Q,R$) 에 대한 평면의 법선 벡터를 구해보자.

법선 벡터를 구하는 방법은 두 벡터의 외적을 이용하면 된다.

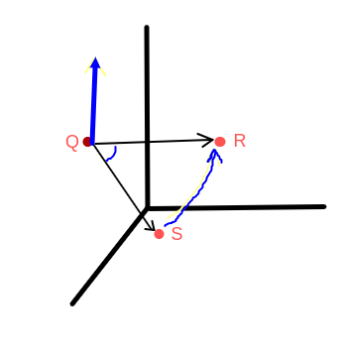
평면위 점 Q, R, S에 대해 평면의 벡터를 구하기 위해 벡터 $\vec{QS}$, $\vec{QR}$ 의 외적을 구해준다.

$\vec{QS} \times \vec{QR}=$ 파란색 벡터 (법선 벡터).

조금 더 첨언을 하자면, 외적을 하게되면 해당 두 벡터와 수직이 되는 벡터를 구하게 된다.

그런데 두 벡터와 수직이 되는 벡터는 총 두 개이다. (방향이 위인 벡터와 아래인 벡터).

나도 처음에는 헷갈렸지만, 외적을 해서 구하게 되는 벡터는 오른나사 법칙을 따르게 된다고 한다.

따라서 QS에서 QR로 시계방향 회전하면서 외적을 하므로, 위를 향하는 법선 벡터를 구하게 되는 것이다.

코드로 나타내면 다음과 같다.

vector<int> q = {q1, q2, q3};
vector<int> r = {r1, r2, r3};
vector<int> s = {s1, s2, s3};

auto qs = s - q;
auto qr = r - q;

auto h = qs * qr; 

이는 간략하게 생성한 것이고, 실제 구현에서는 다르게 구현했다.

법선 벡터를 이용하여 평면을 기준으로 그룹을 나누자

3차원 평면이지만, 편의와 이해를 위해 2차원 형식으로 그려보았다.

(참고로 $\vec{h}$ 는 평면과 수직이므로 주황색 진한 선이 평면을 옆에서 본 모습이다)

특정한 점 X에 대해, 벡터 $\vec{xp}$를 만들어보자, 그리고 $\vec{xp}$와 법선 벡터 $\vec{h}$와의 내적을 구해보자

그러면 벡터는 이동이 자유로으므로, 벡터의 시작점을 $p$ 로 옮겨서 내적을 구하면 값이 양수가 나오게 된다.

반대로 (평면도 기준) 오른쪽에 위치한 점들은 $\vec{xp}$ 가 왼쪽 방향으로 치우칠 것이고 이를 $\vec{h}$와 내적하면 음수가 나올 것이다.

즉 평면을 기준으로 오른쪽에 위치한 점들은 내적값이 음수가 나오고, 왼쪽에 위치한 점들은 내적값이 양수가 나온다.

= 평면을 기준으로 두 그룹을 나눌 수 있게 되었다는 의미이다.

Q. 그러면 평면 위의 점들은 어디 그룹에 속해야하는가?

이는 알 방법이 없다. 따라서 평면 위 3개의 점에 대해서는 모든 경우의 수를 다 파악해봐야한다.

해당 문제는 구현상의 어려움도 존재한다

사람들이 시간 초과를 많이 받은 이유이기도 하다

분산을 구하는 방식에 있어서, 본문에 나온 방식 ((값 - 평균)의 제곱의 합) 이 아니라 다른 방식이 있다.

\[c=\Sigma_{i=3}^n{(r_i-r)^2 + (g_i-g)^2 + (b_i-b)^2 }\]

각각의 실수연산을 하지않고, 분산의 공식을 (잘) 응용하여 해결하면 시간 초과를 안 받을 수 있다.

사실 이는 생각도 못할 뻔 했는데
jinhan814 님의 질문글과
sait2000 님의 답변 덕에 생각할 수 있었다.

Solved Code

#include <bits/stdc++.h>
#define int long long

using namespace std;
typedef pair<int, int> pii;

int n, k;
int points[101][3];      // 모든 점들이 저장됨
int where[100];          // i-점의 사용 세탁기 번호
double washer[2][2][3];  // 익스트림 여부, 세탁기 번호, RGB 번호
double cnt[2];           // i-세탁기의 세탁물 개수
bool visited[100];       // 해당 점이 평면 위에 있는 지 여부
int pqr[3];              // 평면 위 좌표 3개
int var[3];              // 함수 종료 전달인자
double result = DBL_MAX;
// i번 째 세탁물을 세탁기에 집어 넣음
void push(int i) {
  int washer_num = where[i];
  cnt[washer_num] += 1;
  for (int rgb = 0; rgb < 3; ++rgb) {
    washer[0][washer_num][rgb] += points[i][rgb];
    washer[1][washer_num][rgb] += (points[i][rgb] * points[i][rgb]);
  }
}

// i번 째 세탁물을 세탁기에서 빼냄
void pull(int i) {
  int washer_num = where[i];
  cnt[washer_num] -= 1;
  for (int rgb = 0; rgb < 3; ++rgb) {
    washer[0][washer_num][rgb] -= points[i][rgb];
    washer[1][washer_num][rgb] -= (points[i][rgb] * points[i][rgb]);
  }
}

// i-세탁기의 세탁물 결과를 반환함.
double calc(int washer_num) {
  double ret = 0.0;
  // 0 으로 나눠지는 것을 방지
  if (cnt[washer_num] == 0) return ret;
  for (int rgb = 0; rgb < 3; ++rgb) {
    ret += washer[1][washer_num][rgb] -
           (washer[0][washer_num][rgb] * washer[0][washer_num][rgb] /
            cnt[washer_num]);
  }
  return ret;
}

// 세탁기 비우기
void clear() {
  for (int i = 0; i < 2; ++i)
    for (int j = 0; j < 2; ++j)
      for (int m = 0; m < 3; ++m) washer[i][j][m] = 0.0;
  cnt[0] = cnt[1] = 0;
}

// i번 째, j번 째 점들을 통과하는 벡터를 생성함 (var에 전달)
void get_vector(int i, int j) {
  for (int m = 0; m < 3; ++m) var[m] = points[j][m] - points[i][m];
}

// i번 째, j번 째 점의 외적 벡터를 구함 (var에 전달)
void get_outer(const vector<int> &i, const vector<int> &j) {
  for (int m = 0; m < 3; ++m)
    var[m] = i[(m + 1) % 3] * j[(m + 2) % 3] - i[(m + 2) % 3] * j[(m + 1) % 3];
}

// 해당 벡터와 내적한 값이 양인지 음수인지 판별 후 저장
void get_where(int who, const vector<int> &h) {
  int ret = 0;
  for (int i = 0; i < 3; ++i) ret += h[i] * var[i];
  where[who] = ret > 0;
}

// 외적 벡터를 구해서 어디에 넣어야 하는 지 구분지음.
void solve() {
  get_vector(pqr[0], pqr[1]);
  vector<int> pq = {var[0], var[1], var[2]};
  get_vector(pqr[0], pqr[2]);
  vector<int> pr = {var[0], var[1], var[2]};
  get_outer(pq, pr);
  vector<int> h = {var[0], var[1], var[2]};

  // 세탁기 비우기
  clear();
  for (int i = 0; i < n; ++i) {
    // pqr 에 대해서는 나중에 처리하도록 함.
    if (visited[i]) continue;
    get_vector(pqr[0], i);
    get_where(i, h);
    push(i);  // 그리고 다 넣음.
  }
  // 이제 pqr에 대해 처리하기
  for (int i = 0; i < (1 << 3); ++i) {
    for (int j = 0; j < 3; ++j) {
      where[pqr[j]] = (i & (1 << j) ? 1 : 0);
      push(pqr[j]);
    }
    // cout << calc(0) + calc(1) << '\n';
    result = min(result, calc(0) + calc(1));
    for (int j = 0; j < 3; ++j) pull(pqr[j]);
  }
}

// 점 3개를 선택하는 경우의 수 생성
// 결과는 pqr에 저장되며 3개가 모두 선택시 solve() 함수로 이동
void dfs(int index, int depth) {
  if (depth == 3) {
    // 선택 종료 및 정답 찾기 수행
    solve();
    return;
  }
  // index 번 째 부터 끝까지 선택 수행
  for (int i = index; i < n; ++i) {
    if (visited[i]) continue;
    visited[i] = true;
    pqr[depth] = i;
    dfs(i + 1, depth + 1);
    visited[i] = false;
  }
}

int32_t main(void) {
#ifndef ONLINE_JUDGE
  freopen("input.txt", "r", stdin);
  freopen("output.txt", "w", stdout);
#endif  // ONLINE_JUDGE
  ios_base::sync_with_stdio(false);
  cin.tie(nullptr);
  cout.tie(nullptr);
  cout << fixed;
  cout.precision(6);

  cin >> n >> k;
  for (int i = 0; i < n; ++i)
    for (int j = 0; j < 3; ++j) cin >> points[i][j];
  if (k == 1) {
    // 같은 세탁기를 사용해야하므로 바로 답을 구함
    for (int i = 0; i < n; ++i) push(i);  // 모든 세탁물을 세탁기에 넣음
    cout << calc(0) << '\n';              // 나온 결과를 출력
    return 0;
  }
  if (n < 3) {
    // 2개 또는 1개는 그냥 각각 돌리면 됨. 섞일 방법이 없음.
    cout << 0.0 << '\n';
    return 0;
  }
  // 실제로 처리
  dfs(0, 0);
  cout << result << '\n';
  return 0;
}